walotta的灾后重建规划（单调栈运用）

原题

题目描述

上回说到，walotta同学很喜欢他的 $n\times m$ 大小的箱庭式全自动灌溉收割一体化农场，但是在收获的途中，快乐的他蹦蹦跳跳的把一部分田地踩坏了！

对于单块未被踩坏的地，walotta同学统计它还在多少块完整的且全部未被踩坏的矩形田地中，并称这个数量为方案数。现在walotta想要统计出所有未被踩坏的田地的方案数总和，请你帮帮他吧！

输入格式

第一行输入两个数 $n$, $m$

接下来的 $n$ 行，每行输入 $m$ 个字符，# 代表被踩坏的田地，.代表未被踩坏的田地

输出格式

仅一行，输出总的方案数

样例输入

3 4
..#.
#...
...#

样例输出

40

数据范围

对于100%的数据有 $0<n,m\leq 2000$

原始思路

按照最原始的描述去计算每个格子在多少矩形中显然是不太可行的，第一是时间复杂度过高，第二是实现起来也很复杂。

那么不妨转换一下思路，格子被矩形包含，实质上就是矩形包含格子，那么我们不妨从矩形的角度考虑，只要计算每个矩形包含了多少个格子，就得到了得到这个矩形的对答案的贡献。具体一点，我们枚举所有矩形，对于不包含#的矩形，将其面积累计到答案中；对于包含#的矩形，对答案的贡献为0。

在实现细节上，我们可以用二维前缀和维护矩形中包含的#的数量，从而$O(1)$地判断某个矩形中是否含有#。这样总的时间复杂度就是枚举矩形的时间复杂度，为$O(n^2m^2)$，但值得一提的是，由于存在一个小小的剪枝（具体参见下面代码），实际的时间复杂度达不到$O(n^2m^2)$的级别。

剪枝后甚至能过掉$0<n,m\leq 300$的数据点，而不剪显然是过不了的

下面贴出代码：

代码仅供参考，请不要盲目抄袭代码来完成作业！！！

#include <iostream>

using namespace std;

int n, m;
int sum[2010][2010], after[2010][2010];
char mmap[2010][2010];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> mmap[i][j];
        }
    }
    // 二维前缀和维护#的数目
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + (mmap[i][j] == '#');
        }
    }

    long long ans = 0;  // 得开long long！
    for (int i = 1; i <= n; i++) {  // 四重循环枚举正方形的左上角点和右下角点
        for (int j = 1; j <= m; j++) {
            for (int s = i; s <= n; s++) {
                for (int t = j; t <= m; t++) {
                    if (sum[s][t] - sum[i - 1][t] - sum[s][j - 1] + sum[i - 1][j - 1] == 0) {
                        ans += (s - i + 1) * (t - j + 1);
                    } else {
                        break;  // 如果这个矩形中已经包含了#，那么右下角点的列数再变大也会包含#，故可以break
                    }
                }
            }
        }
    }
    cout << ans;
    return 0;
}

单调栈

首先，为了下面的叙述方便，我们将不包含#的矩形称作合法矩形。

上面的想法十分不错，但问题在于不必要的枚举次数太多，假设我们已经得到了一个大的合法矩形，那么其中的小矩形必定合法，并且不需要再被枚举，而是可以用数学方法直接计算其面积和，也就是说，我们只需要得到“最大”的那些合法矩形的面积即可。

这里“最大”矩形就是指该合法矩形不被其他合法矩形所包含

但是“最大”这个概念有些模糊，很难去找出这种矩形，那么我们不妨提供一些限制条件，比如给定它的某一条边。我们考虑所有给定底边的矩形，这样我们就只用考虑如下图所示的形状（绿色为合法矩形，红色为#）

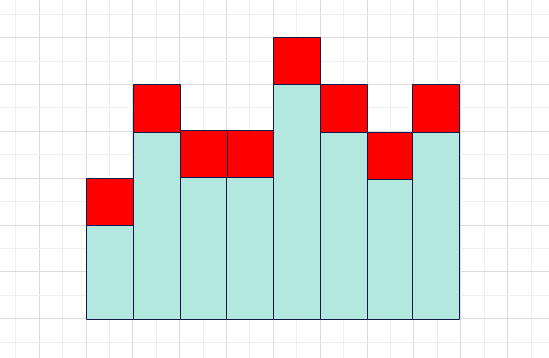
有了这种限制，我们就可以一列一列地往后枚举，并且统计出以每一列的绿色矩形结尾的最大矩形（比如对于第六列的矩形来说，就是下图中的蓝色部分）。

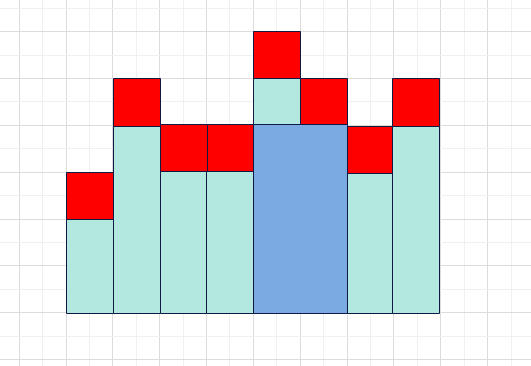
虽然这样看来可能所维护的未必是真正的“最大”矩形（毕竟给定的底边下面可能还有合法部分），但是本文最后我们会知道，这种重复带来的复杂度是可接受的。

我们考虑以第$i$行的方块为底边，并设每一列的宽度为$1$的最高的合法矩形高度为$height_{ij}$（即上图每一列的绿色矩形的高度，方便起见，下面的叙述中简记为$height_j$）。可以想象，如果$height_{j-1} > height_{j}$，那么对于以$j$后面的列结尾的最大矩形来说，$height_{j-1}$显然不会再造成限制。由此看来，我们需要维护一个关于$height_j$单调递增的结构。

具体来说，我们希望维护一个关于$height_j$单调递增的单调栈，栈顶记为$height_{top}$，对应的以栈顶元素结尾的最大矩形宽度为$width_{top}$，当$height_j$要入栈时，如果$height_{top}>height_j$，那么应该将$height_{top}$出栈。但是$width$应该怎么维护呢？直接将$width_{top}$加到$width_{j}$上吗？不对！

这个问题并不那么简单，考虑下面的形状

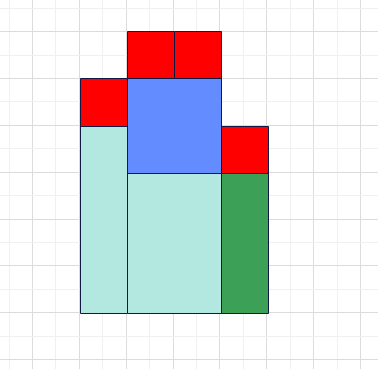
深绿色的是当前入栈的那一列，即$height_j$，如果直接计算$height_{top}$比$height_{j}$高出去的那部分的贡献并且删除它（即图中蓝色的部分），那么答案是不正确的！这会使得下图中蓝色的部分（以及包含它的一些矩形）没有被计算！

由此看来，应该将将$width_{top}$合并到$width_{top-1}$和$width_j$中的一个，具体取决与$height_{top-1}$和$height_{j}$的大小。形象化来说，把$height_{top}$对应的最大矩形的高度削平到左右相邻高度中较大的一个，即删除下图中的蓝色部分

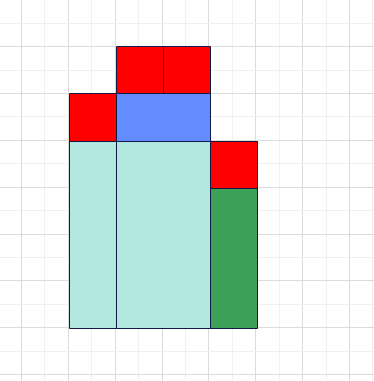
我们再完整地叙述一下算法流程：
具体来说，我们希望维护一个关于$height_j$单调递增的单调栈，当$height_j$要入栈时，如果$height_{top}>height_j$，那么将$height_{top-1}$和$height_{j}$进行比较，若$height_{j}>height_{top-1}$，则将$width_{j}$加上$width_{top}$；反之，则将$width_{top-1}$加上$width_{top}$，维护完$width$后，还要在答案中累计$height_{top}$比$height_j$或$height_{top-1}$高的那部分的贡献。如此重复操作，直到栈满足单调增性质。

$height_{top}$比$height_j$或$height_{top-1}$低的那部分已经累计到以$height_{j}$结尾的最大矩形里了，会在以后统计进去

最后一列处理完后，我们可能还会有一些关于$height$单调递增的元素残留在单调栈中，我们只需要把栈中元素依次出栈，按照上面的规则计算贡献即可。

前面我们一直忽略了具体计算的数学公式，现在我们来推导它。我们希望计算出被删除区域的贡献。比如对于下图蓝色的被删除区域，它的贡献就是右边两个黄色矩形的面积和。

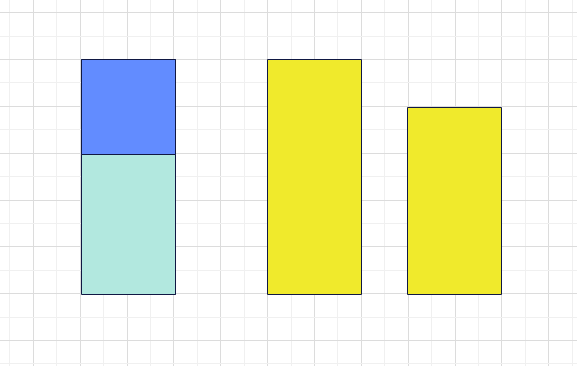
假设矩形底边宽$w$，蓝色部分高度为$low$到$high$。我们先考虑在底边上任意取小线段，长度为$1$的线段有$w$条，长度为$2$的有$w-1$条，……，长度为$w$的有$1$条，所有线段的总长度和为

$$1\times w+2(w-1)+3(w-2)+\cdots+w\times 1 = \frac{w(w+1)(w+2)}{6}$$

对于每条线段，都可以构成高度为$low$~$high$的矩形，这样所有矩形的面积和就是

$$\frac{w(w+1)(w+2)}{6}\cdot (low+(low+1)+\cdots +high)=\frac{w(w+1)(w+2)(low+high)(high-low+1)}{12}$$

最后分析一下复杂度，枚举每一行作为底边，对于每一行做一遍单调栈操作，总复杂度是$O(mn)$。

下面贴出代码：

代码仅供参考，请不要盲目抄袭代码来完成作业！！！

#include <iostream>

using namespace std;

const int MAXN = 2010;

typedef long long LL;

struct Rect {
    int w, h;
    Rect() : w(0), h(0) { }
    Rect(int _w, int _h) : w(_w), h(_h) { }
};

Rect sta[MAXN];
int n, m;
int height[MAXN][MAXN];  // 以第i行为底，宽1的矩形的最大高度
char mmap[MAXN][MAXN];

inline LL calc(LL w, LL extra, LL base) {  // 这里的base对应上文中的low-1,extra对应(high-low+1)
    return (extra * base + (extra + 1LL) * extra / 2LL) * w * (w + 1) * (w + 2) / 6LL;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            cin >> mmap[i][j];
        }
    }

    // 预处理出height
    for (int j = 0; j < m; j++) {
        height[0][j] = (mmap[0][j] == '.');
    }
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < m; j++) {
            height[i][j] = mmap[i][j] == '#' ? 0 :
                    height[i - 1][j] + (mmap[i][j] == '.');
        }
    }

    LL ans = 0;
    for (int i = 0; i < n; i++) {  // 枚举底边
        int top = 0;
        for (int j = 0; j < m; j++) {
            int w = 1;  // 这个w相当于w_j
            while (top && sta[top].h >= height[i][j]) {
                int bh = max(sta[top - 1].h, height[i][j]);
                ans += calc(sta[top].w, sta[top].h - bh, bh);  // 高出去的部分的贡献
                if (bh == height[i][j]) {
                    w += sta[top].w;
                } else {
                    sta[top - 1].w += sta[top].w;
                }
                top--;
            }
            sta[++top] = Rect(w, height[i][j]);
        }
        while (top) {  // 将剩余的元素出栈
            ans += calc(sta[top].w, sta[top].h - sta[top - 1].h, sta[top - 1].h);
            if (top > 1) sta[top - 1].w += sta[top].w;
            top--;
        }
    }
    cout << ans;
    return 0;
}

最后的一些思考

事实上$width$并不需要用一个数组来存，只需要用一个变量储存并不断维护即可，具体的做法请读者自行思考。

这绝不是因为笔者懒了写不动了

受笔者知识水平和表达能力所限，有的问题难免解释得或啰嗦或出现疏漏，欢迎在评论区指正